Reflected Diffusion Models
Diffusion models are trained to reverse a stochastic process through score matching. However, a lot of diffusion models rely on a small but critical implementation detail called thresholding. Thresholding projects the sampling process to the data support after each discretized diffusion step, stabilizing generation at the cost of breaking the theoretical framework. Interestingly, as one limits the number of steps to infinity, thresholding converges to a reflected stochastic differential equation. In this blog post, we will be discussing our recent work on Reflected Diffusion Models, which explores this connection to develop a new class of diffusion models which correctly trains for thresholded sampling and respects general boundary constraints.
Introduction
Diffusion models
At their core, diffusion models start by perturbing data on $\mathbb{R}^d$ with a hand-designed “forward” stochastic differential equation (SDE) with fixed coefficients $\mathbf{f}$ and $g$
\(\begin{equation} \mathrm{d} \mathbf{x}_t = \mathbf{f}(\mathbf{x}_t, t) \mathrm{d}t + g(t) \mathrm{d} \mathbf{B}_t \end{equation}\)
taking our initial data distribution $p_0$ to a stationary distribution $p_T$ (normally a simple distribution like a Gaussian). Using time reversed Brownian motion $\overline{\mathbf{B}}_t$ and the score function $\nabla_x \log p_t$, one can construct a corresponding “reverse” SDE which takes $p_T$ to $p_0$:
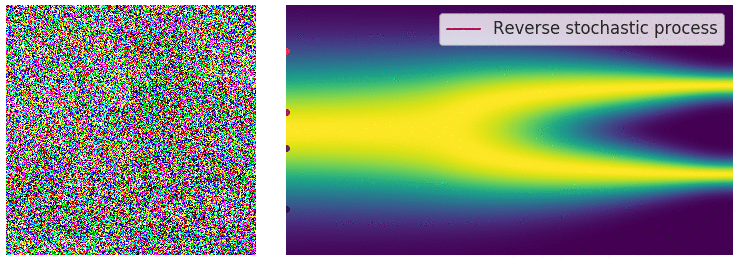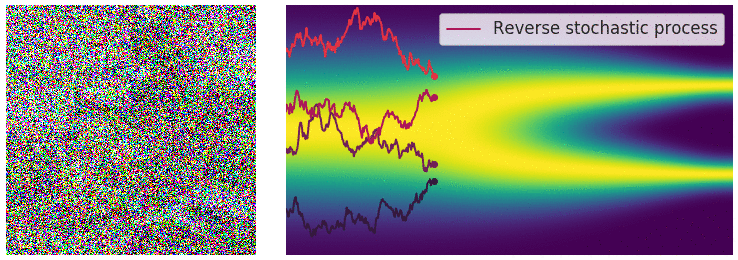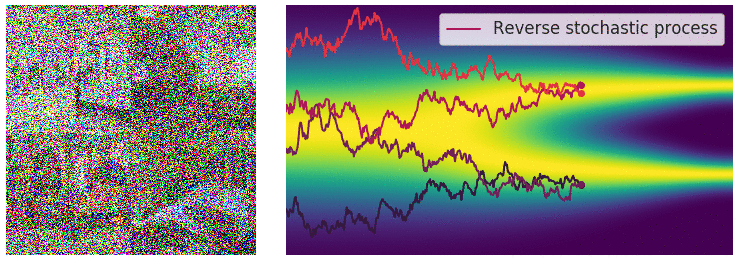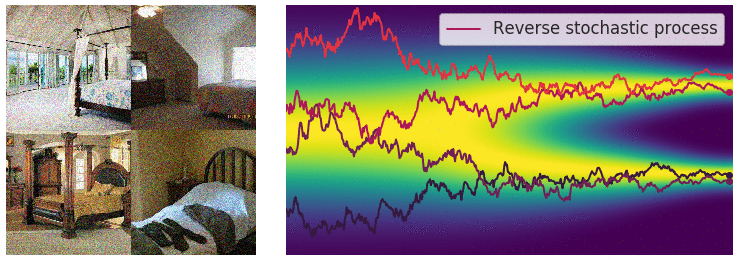
\(\begin{equation} \mathrm{d} \mathbf{x}_t = \left[\mathbf{f}(\mathbf{x}_t, t) - g(t)^2 \nabla_x \log p_t(\mathbf{x}_t) \right]\mathrm{d}t + g(t) \mathrm{d} \overline{\mathbf{B}}_t \end{equation}\)
This defines a stochastic transport from our simple distribution $p_T$ to our data distribution $p_0$, so we can build a generative model by approximating this process.
The only unknown component is the score function $\nabla_x \log p_t$, which can be learned with a time-dependent score neural network $\mathbf{s}_\theta(\mathbf{x}, t)$. To train, we optimize what is known as the score matching loss
which has several equivalent (but tractable) alternative forms (see Yang’s excellent blog post for an overview). Here, $\lambda_t$ is a weighting function that alters the final model’s behavior. For example, setting $\lambda_t = g(t)^2$ maximizes the log-likelihood of the generated data
Thresholding
Unfortunately, the devil always lies in the details. We need to discretize time to simulate the generative SDE, resulting in an Euler-Maruyama scheme with i.i.d. Brownian increments $\mathbf{B}_{\Delta t}^t \sim \mathcal{N}(0, \Delta t)$:
\[\begin{equation} \mathbf{x}_{t - \Delta t} = \mathbf{x}_{t} - \left[\mathbf{f}(\mathbf{x}_t, t) - g(t)^2 s_\theta(\mathbf{x}_t, t) \right] \Delta t + g(t) \mathbf{B}_{\Delta t}^t \end{equation}\]Numerical error can arise from the discretization, the learned score function, or just plain bad luck when sampling the increments, causing our trajectory $\mathbf{x}_t$ to enter low probability regions. Since we train with the Monte Carlo version of our loss
\[\begin{equation} \frac{1}{nm} \sum_{i = 1}^{n} \sum_{j = 1}^m \ \lambda_{t_i} \| \mathbf{s}_\theta(\mathbf{x}_{t_i}^j, t_i) - \nabla_x \log p_{t_i}(\mathbf{x}_{t_i}^j)\|^2 \end{equation}\]it is even possible to never optimize in low probability regions, so the score network behavior there tends to be undefined. Previously, this problem appeared for vanilla score matching, degrading the performance of naive Langevin dynamics


Diffusion models were initially motivated as a stack of VAEs which gradually denoised the input
inspiring a natural fix. We seek to generate images, so the predicted mean $\overline{\mathbf{x}}_{t - \Delta t}$ should be a “valid” image. This can be accomplished by clipping each pixel to the fixed $[0, 255]$ range (which can be rescaled to $[0, 1]$ or $[-1, 1]$ depending on the context), and this trick is known as thresholding. You can find many examples of it in the repositories of famous papers, although it is almost never mentioned:
Thresholding avoids the divergent behavior we saw previously, generating much nicer samples.


Unfortunately, diffusion models are supposed to reverse the forward corrupting process. Changing the generative process like this breaks the fundamental assumption, resulting in a mismatch. This has been linked with phenomena like oversaturation when using a large amount of diffusion guidance (such as in the Imagen generated example), necessitating task-specific techniques that don’t generalize, such as dynamic thresholding

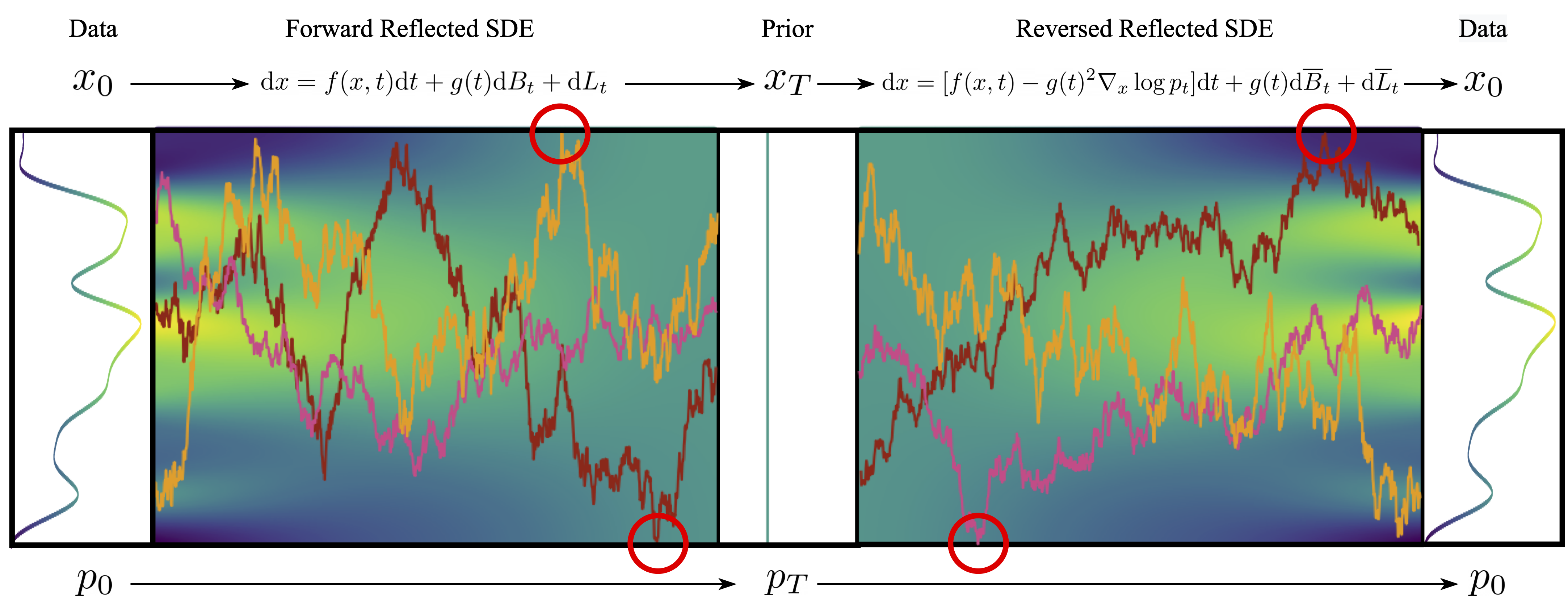
Reflected Diffusion Models
As we take $\Delta t \to 0$, the thresholded Euler Maruyama scheme
\[\begin{equation} \mathbf{x}_{t + \Delta t} = \mathrm{proj}\left(\mathbf{x}_{t} + \mathbf{f}(\mathbf{x}_t, t) \Delta t\right) + g(t) \mathbf{B}_{\Delta t}^t \end{equation}\]converges to what’s known as a reflected stochastic differential equation
The behavior is exactly the same on the interior of our domain, but, at the boundary, the new term $\mathbf{L}_t$ “zeroes out” all outward pointing force to ensure the particle stays within the constraints.

Similar to standard stochastic differential equations, it is possible to reverse this with a reverse reflected stochastic differential equation
\[\begin{equation} \mathrm{d} \mathbf{x}_t = \left[\mathbf{f}(\mathbf{x}_t, t) - g(t)^2 \nabla_x \log p_t \right]\mathrm{d}t + g(t) \mathrm{d} \overline{\mathbf{B}}_t + \mathrm{d} \overline{\mathbf{L}}_t \end{equation}\]This forms the same forward/reverse coupling that undergirds standard diffusion models, so we can use this principle to define Reflected Diffusion Models.
Score Matching on Bounded Domains
To construct our Reflected Diffusion Models, we need to learn $\nabla_x \log p_t$. These are the marginal scores recovered from the forward reflected SDE, not the standard forward SDE. The score matching loss can be made more tractable by employing the denoising trick from standard diffusion models, reducing our loss to a (weighted combination) of denoising score matching losses for each $p_t$
\[\begin{equation} \mathbb{E}_{\mathbf{x} \sim p_0} \mathbb{E}_{\mathbf{x}_t \sim p_t(\cdot \vert x_0)} \| \mathbf{s}_\theta(\mathbf{x}_t, t) - \nabla_x \log p_t(\mathbf{x}_t | \mathbf{x}_0)\|^2 \end{equation}\]One still needs to accurately compute the transition density $p_t(\mathbf{x}_t \vert \mathbf{x}_0)$ quickly, which is not available in closed form. In particular, $p_t(\mathbf{x}_t \vert \mathbf{x}_0)$ is actually a reflected Gaussian variable, and this leads to two natural computation strategies:
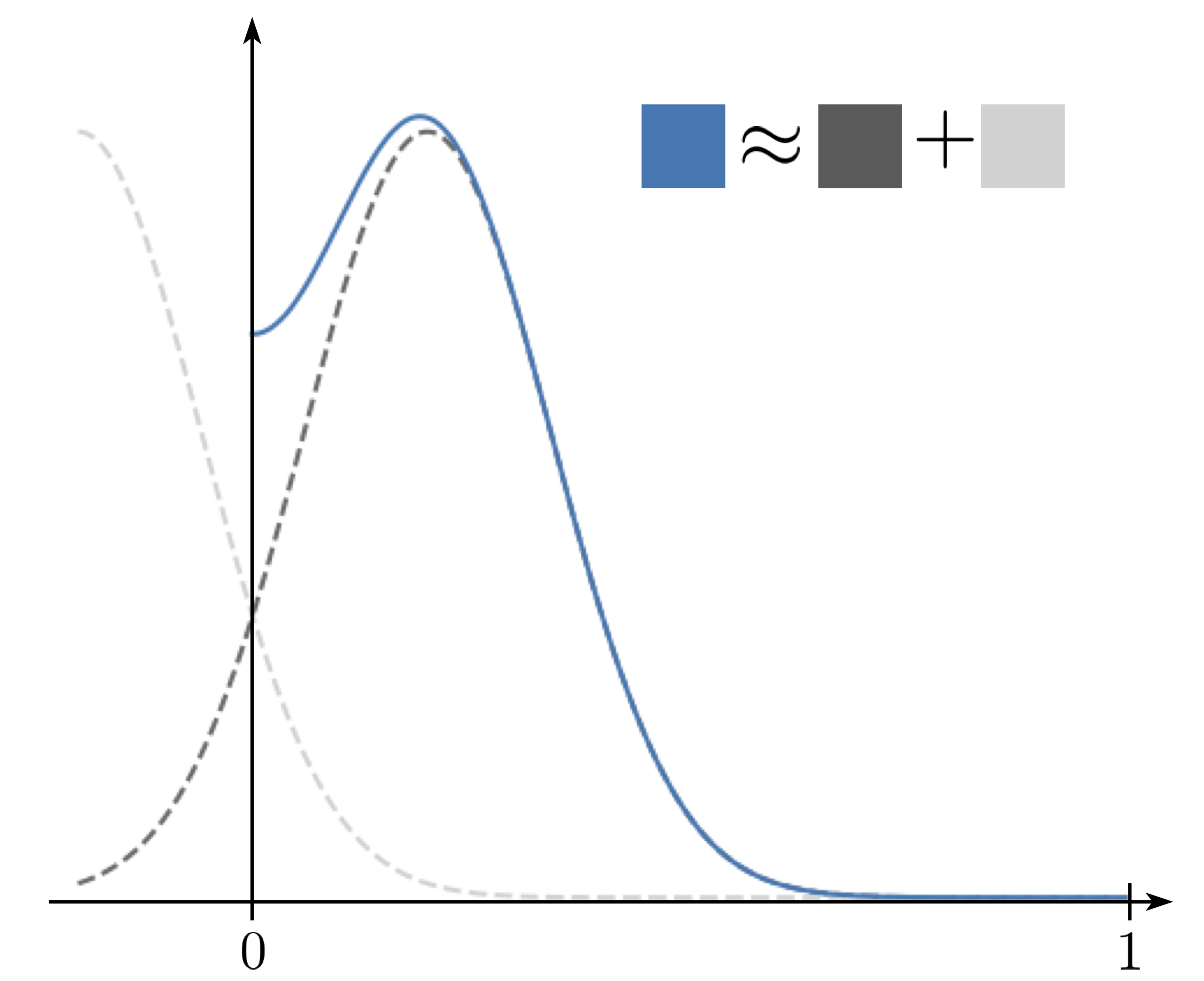
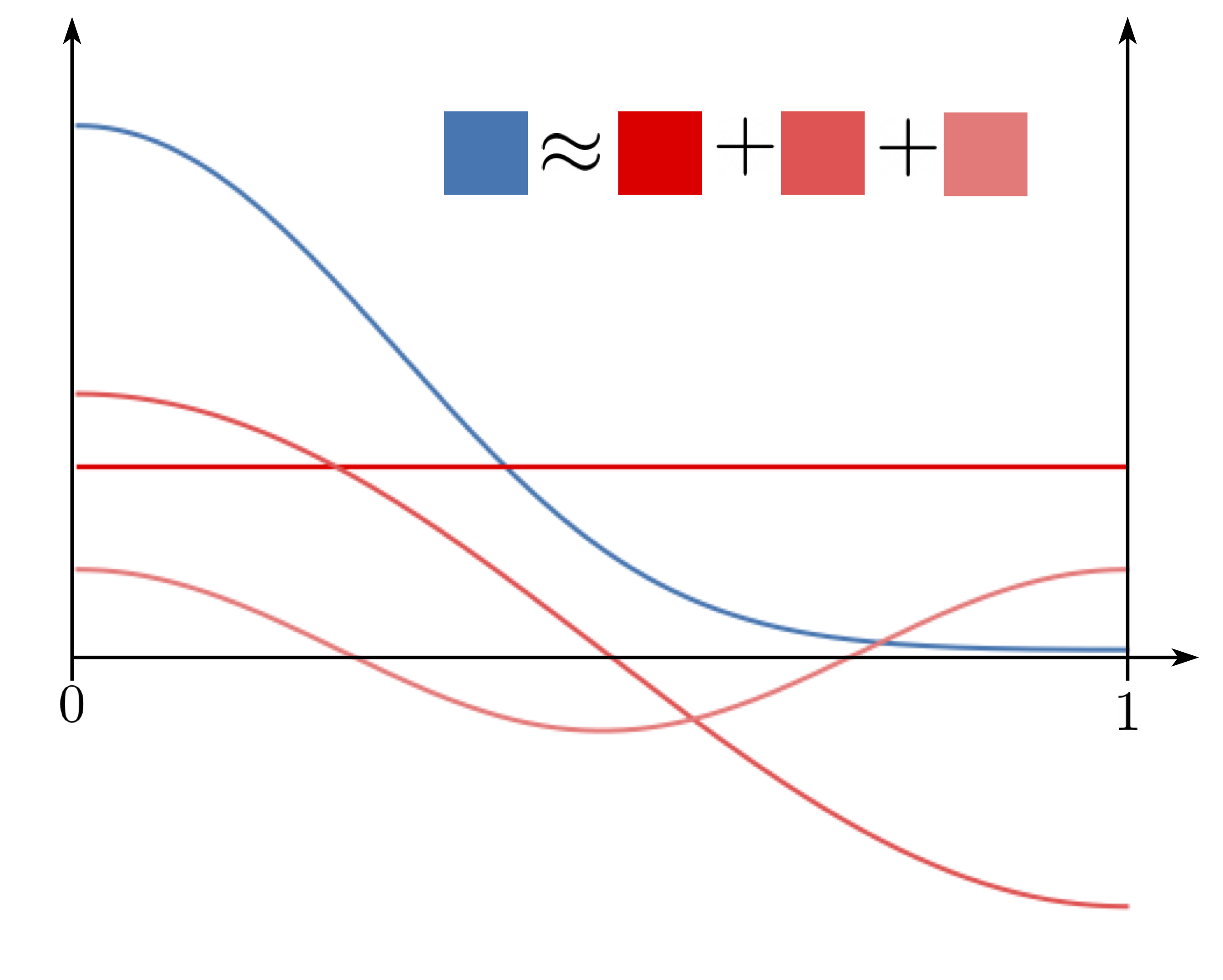
Strategy 1 is accurate for small times since we don’t need to compute as many reflections, while strategy 2 is accurate for large times since the distribution goes closer to uniform, requiring fewer harmonic components. These strategies shore up the other’s weaknesses, so we combine them to efficiently compute the transition density.
How to Solve Reverse Reflected SDEs
We have already seen that thresholding provides a Euler-Maruyama type discretization. The core idea is that it approximates $\mathbf{L}_t$ in discrete time. However, we are by no means limited to just thresholding. We found that approximating the process with a reflection term produced better samples:
\[\begin{equation} \mathbf{x}_{t - \Delta t} = \mathrm{refl}\left(\mathbf{x}_{t} - \left[\mathbf{f}(\mathbf{x}_t, t) - g(t)^2 \mathbf{s}_\theta(\mathbf{x}_t, t) \right] \Delta t + g(t) \mathbf{B}_{\Delta t}^t\right) \end{equation}\]This produces reasonable samples, but we can actually further augment the sampling procedure. Since $\mathbf{x}_t \sim p_t$, we can use our score function to define a predictor-corrector update scheme based on Constrained Langevin Dynamics to “correct” our sample $\mathbf{x}_t$:
\[\begin{equation} \mathrm{d} \mathbf{x}_t = \frac{1}{2} s_\theta(\mathbf{x}_t, t) \mathrm{d} t + \mathrm{d} \mathbf{B}_t + \mathbf{L}_t \end{equation}\]With this component, we match all of the constructs from standard diffusion models. We can achieve state-of-the-art perceptual quality (as measured by Inception score) without modifying the architecture or any other components. Unfortunately, the FID score, another common metric, tends to lag behind because our generated samples have noise (at the scale of 1-2 pixels) that FID is notoriously sensitive to.
| Method | Inception score (↑) |
|---|---|
| NCSN++ | 9.89 |
| Subspace Diffusion | 9.99 |
| Ours | 10.42 |
Probability Flow ODE
Analogous to the widely used DDIM scheme
This results in a reflected diffusion process that has the same marginal probabilities as our original SDE, and allows us to sample with a lower variance. Amazingly, as we take $\overline{g}(t) \to 0$, the boundary reflection term $\mathrm{d} \mathbf{L}_t$ disappears since $\nabla_x \log p_t$ satisfies Neumann boundary conditions:
\[\begin{equation} \mathrm{d} \mathbf{x}_t = \left[\mathbf{f}(\mathbf{x}_t, t) - \frac{g(t)^2}{2} \nabla_x \log p_t(\mathbf{x}_t)\right]\mathrm{d}t \end{equation}\]We can replace $\nabla_x \log p_t$ with our score function approximation $\mathbf{s}_\theta$ to recover a Probability Flow ODE
Interestingly, learning with the $\lambda_t$ weighting function that we used for image generation results in an ELBO, so we can use the same noise schedule to generate good images and maximize likelihoods. When compared with other likelihood-based diffusion methods, our optimization has much lower variance, so we can achieve likelihood results that are close to the state of the art without requiring either importance sampling or a learned noise schedule.
| Method | CIFAR-10 BPD (↓) | ImageNet-32 BPD (↓) | |
|---|---|---|---|
| ScoreFlow | 2.86 | 3.83 | |
| (with importance sampling) | 2.83 | 3.76 | |
| VDM | 2.70 | —— | |
| (with learned noise) | 2.65 | 3.72 | |
| Ours | 2.68 | 3.74 |
Diffusion Guidance
One of the major perks of diffusion models is their controllability. Using some conditional information $\mathbf{c}$, which could be the class or a piece of description text, we can guide samples to satisfy $c$ through a classifier $p(\mathbf{c} \vert \mathbf{x})$:
\[\begin{equation} \nabla \log p_t(\mathbf{x} \vert c) = \nabla \log p_t(\mathbf{x}) + \nabla \log p_t(c \vert \mathbf{x}) \end{equation}\]Currently, this notion of controllable diffusion normally appears as classifier-free diffusion guidance
In the literature, increasing $w$ generates more fidelitous images, which is crucial for text-to-image guided diffusion. From our experiments, we found that thresholding is critical for classifier-free guidance to work. Without it, sampling with even small weights $w$ causes images to diverge:

Additionally, we can’t use quick deterministic ODE sampling methods since we can’t mimic the effect of thresholding. In fact, this seems to cause samples to diverge even more:

Furthermore, although a large guidance weight $w$ is preferred in applications such as text-to-image diffusion, it is well known that this can cause samples to suffer artifacts such as oversaturation even when thresholding.

We hypothesize that this these artifacts are due to the mismatch between training and sampling. In particular, the trained behavior seeks to push samples out-of-bounds, and the sampling procedure clips these out-of-bounds pixels to $0$ or $255$, resulting in oversaturation. Because Reflected Diffusion Models are trained to avoid this behavior, our high guidance weight samples are significantly less saturated and do not contain any artifacts:

Lastly, when we combine score networks for classifier-free guidance, the Neumann boundary condition is maintained. As such, it is possible to sample from classifier-free guided diffusion models using our Probability Flow ODE, requiring far fewer evaluations.

Generalizing to Different Geometries
We have constructed our framework to be completely general with respect to the underlying domain $\Omega$. As such, we can apply our model to a wider variety of domains beyond the hypercube (which we used to model images):

For instance, applying Reflected Diffusion Models to simplices results in a simplex diffusion method that learn in high dimensions. We did not explore this further, but in principle, this opens up potential applications in fields such as language modeling.
Conclusion
This blog post presented a detailed overview of our recent work “Reflected Diffusion Models”. Our full paper can be found on arxiv and contains many more mathematical details, additional results, and deeper explanations. We have also released code.